极端值如何影响线性回归模型
极端值如何影响线性回归模型
线性回归的作用:拟合数据,预测关系。
数据中常有极端值,可能会影响预测结果。
一元线性回归模型
假设目标变量 $y$与自变量 $x$存在线性关系:
$y=\beta_0+\beta_1x+\epsilon$
这里总假定 $x$为一般变量,是非随机变量,其值是可以精确测量或严格控制的。$\beta_0,\beta_1$为未知参数,$\beta_1$是直线的斜率,$\epsilon$ 是随机误差,通常假定:
$E(\epsilon)=0$,$Var(\epsilon)=\sigma^2$,
在对未知参数做区间估计或假设性检验时还需假定误差服从正态分布,即:
$y\sim N(\beta_0+\beta_1x,\sigma^2)$.
由于$\beta_0,\beta_1$均未知,需要我们从收集到的数据$(x_i,y_i)(i=1,2,…,n)$出发进行估计。在收集数据时,一般要求观测独立地进行,即假定$y_1,y_2,…,y_n$相互,独立.综合上述诸项假定,我们给出最简单最常用的一元线性回归的统计模型:
$y_i=\beta_0+\beta_1x_i+\epsilon_i$ ,$i=1,2,…,n$,
各$\epsilon_i$独立同分布,其分布为$\mathcal{N}(0,\sigma^2)$
由数据$(x_i,y_i)(i=1,2,…n)$可以获得$\beta_0,\beta_1$的估计$\hat{\beta_0}$,$\hat{\beta_1}$, 称
$\hat{y}=\hat{\beta_0}+\hat{\beta_1}x$
为$y$关于$x$的经验回归函数,简称回归方程,其图形称为回归直线。给定$x=x_0$后,称$\hat{y_0}=\hat{\beta_0}+\hat{\beta_1}x_0$为回归值(也称为拟合值、预测值).
回归系数的最小二乘估计(Ordinary Least Squares, OLS)
一般采用最小二乘法估计模型中的$\beta_0,\beta_1$,令 $Q(\beta_0,\beta_1)=\sum_{i=1}^{n}(y_i-{\beta_0}-\beta_1x_i)^2$,
最小二乘的核心原理是最小化误差平方和 $Q(\beta_0,\beta_1)$
假设有一个极端点$(x_n,y_n)$,它的$y_n$远大于其它点。对于这个点,其误差$\epsilon_n=y_n-\beta_0-\beta_1x_n$ 会非常大,由于$Q$ 是误差的平方和,在平方和的放大作用下,误差会变得极其巨大,以至于在$Q$ 中占据了主导地位。那么,为了让$Q$ 达到理想的最小值,就会优先考虑这个极端点,尽可能“拉近”与极端点的距离,使得误差平方和最小,同时,这个过程影响其他“正常”点的拟合。
eg:如果普通样本误差是$1$,贡献是$1^2=1$
如果一个极端值误差是$10$,贡献是$10^2=100$
也就是说,一个极端值的影响力可以是正常值的100倍。
由此可以看出,OLS对极端值非常敏感。
线性回归的一个主要弱点在于它对异常值非常敏感——这些数据点明显偏离整体数据的规律。如果不妥善处理,这些异常值可能会扭曲估计结果、降低预测准确性,并导致无效的推断。
数学推导的直观过程如下:
记
$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$
$\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i$
要求 $Q(\beta_0,\beta_1)=\sum_{i=1}^{n}(y_i-{\beta_0}-\beta_1x_i)^2$ 的最小值,通过对$\beta_0,\beta_1$ 求偏导令其等于$0$ 可得公式:
$\hat{\beta_1} = \frac{\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sum_{i=1}^{n}(x_i-\bar x)^2}$ 含义:分子是$x和y$ 的协方差,分母是$x$ 的方差。
$\hat\beta_0=\bar y-\hat \beta_1x$
对于$\hat\beta_1$ ,极端的$x_i$,$y_i$ 可以显著改变分子或者分母的值(使整体的方差、协方差改变),使得$\hat\beta_1$ 的值严重偏离原来拟合的趋势。
(此时也可以看出,极端值对均值影响也很大,所以在处理某些缺失值和异常值时通常采用众数或中位数替代而不是用均值替代)
有两个概念:
杠杆点(Leverage Points):
- 定义:杠杆点是指在自变量空间中远离其他观测点的样本点。
- 特点:
- 仅看自变量 $x$的分布,而不考虑因变量 $y$。
- 对回归模型的拟合有潜在影响,但不一定改变回归系数。
影响点(Influential Points):
-
定义:影响点是指对回归模型的估计结果(回归系数或预测值)有显著影响的观测点。
特点:
-
同时考虑自变量$x$和因变量 $y$。
-
影响系数估计、拟合线或预测结果。
-
不一定是杠杆点(自变量值不极端,但 $y$异常也可能是影响点)。
-
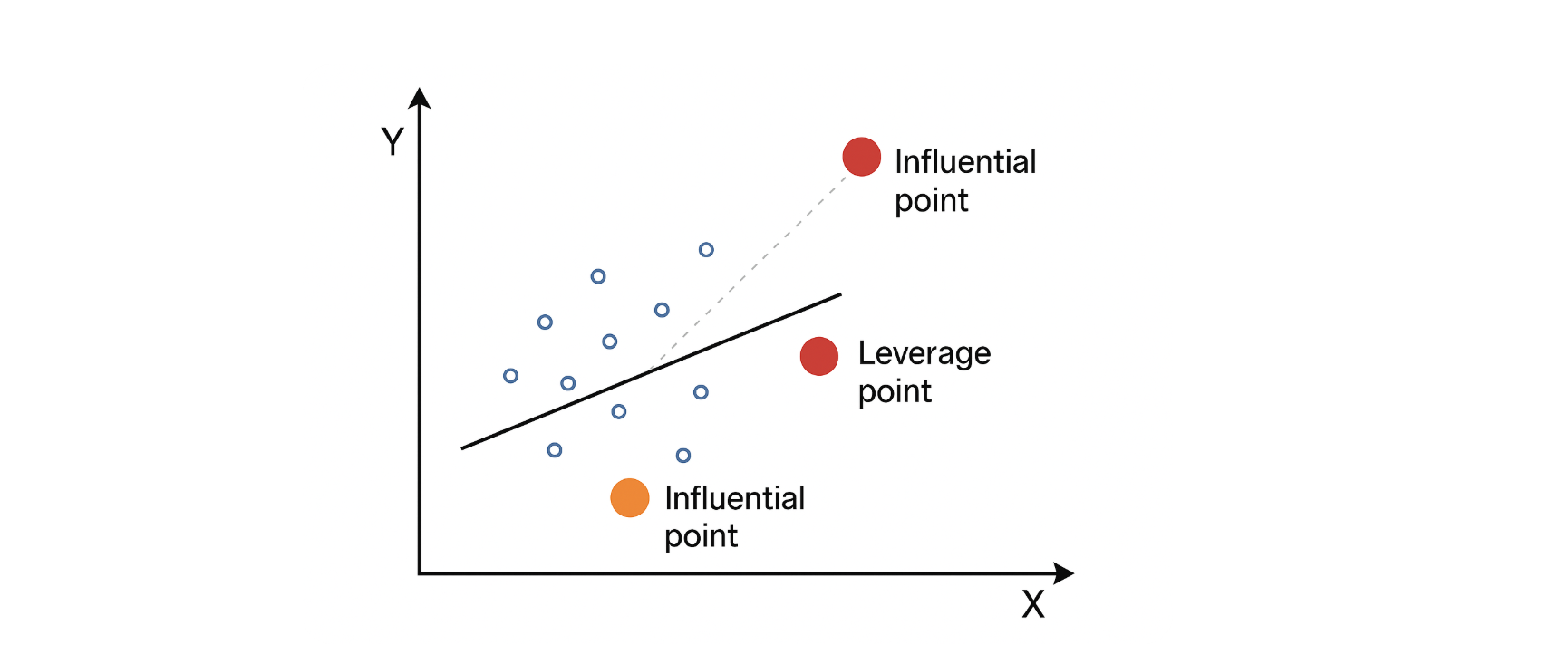
举例说明极端值影响
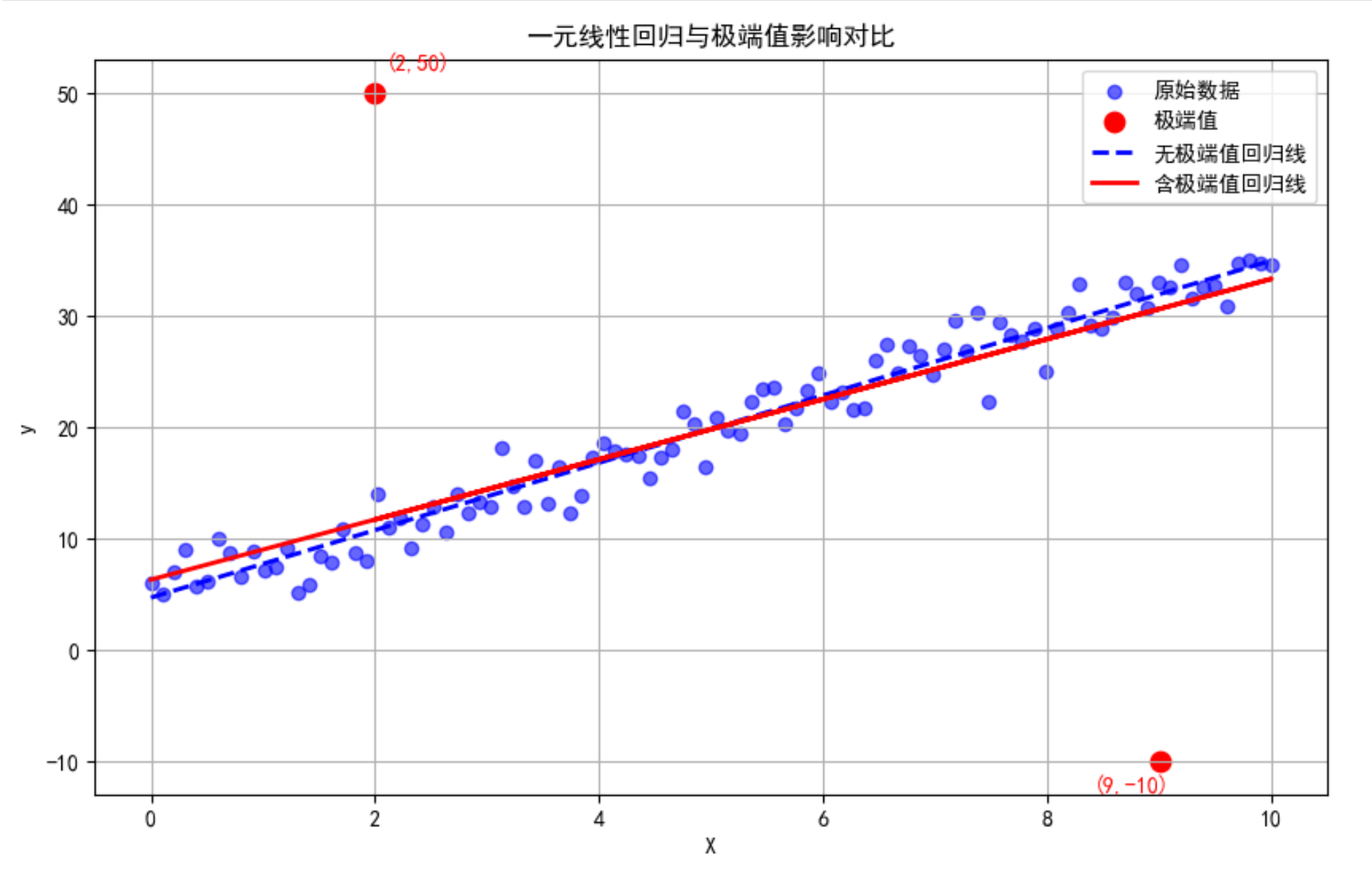

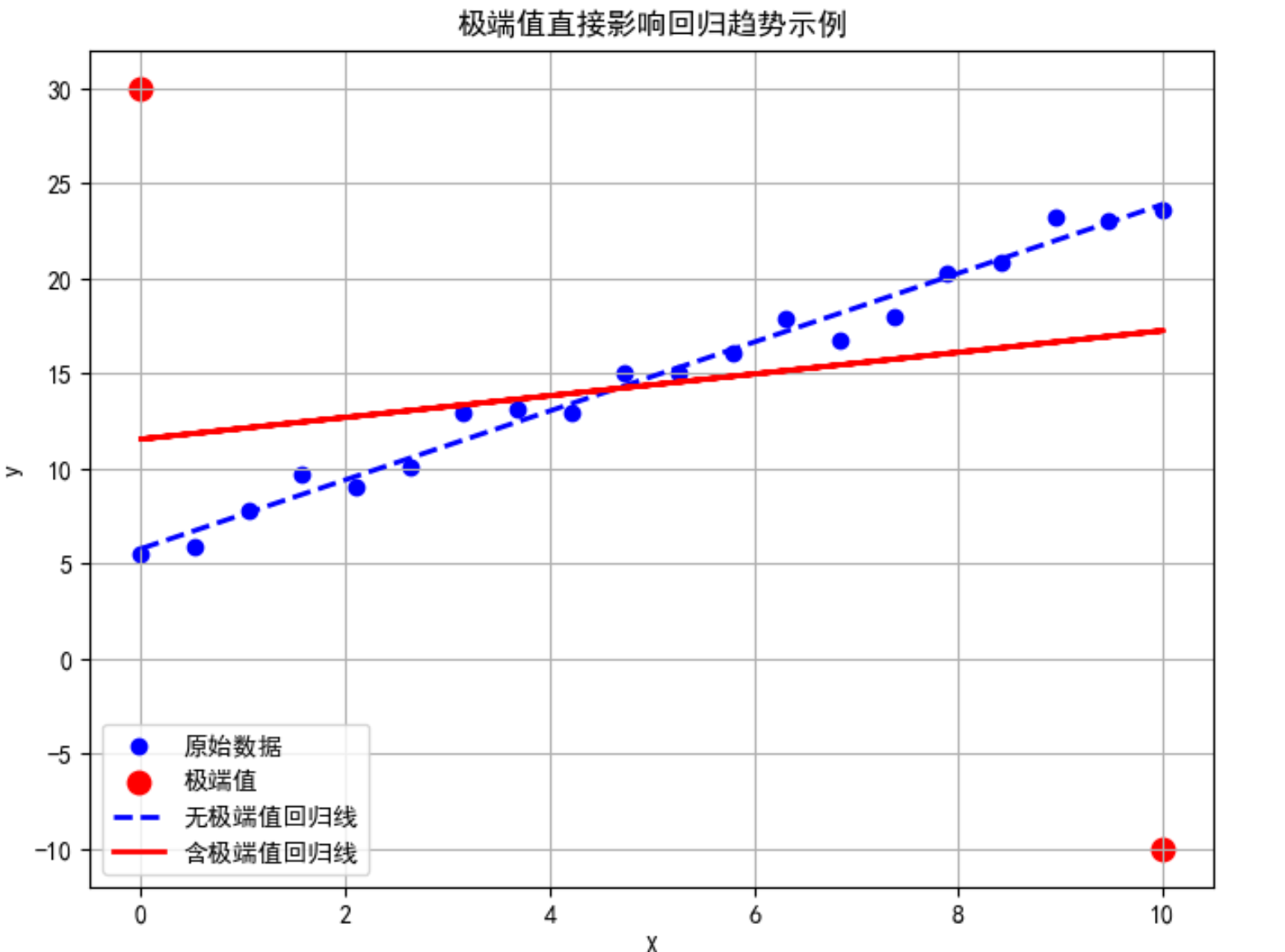
在房价预测模型中,现在假设房价只和居住面积大小有关。
| 居住面积 (㎡) | 房价 (万元) | 单价 (万元/㎡) | 备注 |
|---|---|---|---|
| 50 | 80 | 1.6 | 普通小户型 |
| 100 | 160 | 1.6 | 正常 |
| 150 | 230 | 1.53 | 正常 |
| 200 | 280 | 1.4 | 正常 |
| 250 | 1200 | 4.8 | 顶层复式、极端高价 |
最后一套房(250㎡,1200万)属于极端值。(单价增长趋势是3倍多,总价是4倍多)
计算 $\hat{\beta_1} = \frac{\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sum_{i=1}^{n}(x_i-\bar x)^2}=4.76$
$\hat\beta_0=\bar y-\hat \beta_1x=-324$
回归方程为:$y=-324+4.76x$
看起来没问题,解释起来:
- 斜率$\beta_1$ :面积每增加$1m^2$ ,价格增加4.76万元
- 截距$\beta_0$ :面积为0时,房价为-324万元(显然不符合实际)
- 极端值1200拉大了斜率,原本房价是$1.4$万元/$m^2$ ~$1.6$万元/$m^2$ ,被拉升到4.76万元/$m^2$
取完对数后(取自然对数)
| 原价 (万元) | log(房价) | 说明 |
|---|---|---|
| 80 | 4.38 | 正常值 |
| 160 | 5.08 | 正常值 |
| 230 | 5.44 | 正常值 |
| 280 | 5.63 | 正常值 |
| 1200 | 7.09 | 极端值被“压缩”,与其余几组值差距没有原来那么大 |
此时最后一组数据的总价增长趋势和前面几组差距不大,属于正常趋势范围。
计算 $\hat{\beta_1} = \frac{\sum_{i=1}^{n}(x_i-\bar x)(y_i-\bar y)}{\sum_{i=1}^{n}(x_i-\bar x)^2}=0.012$
$\hat\beta_0=\bar y-\hat \beta_1x=3.731$
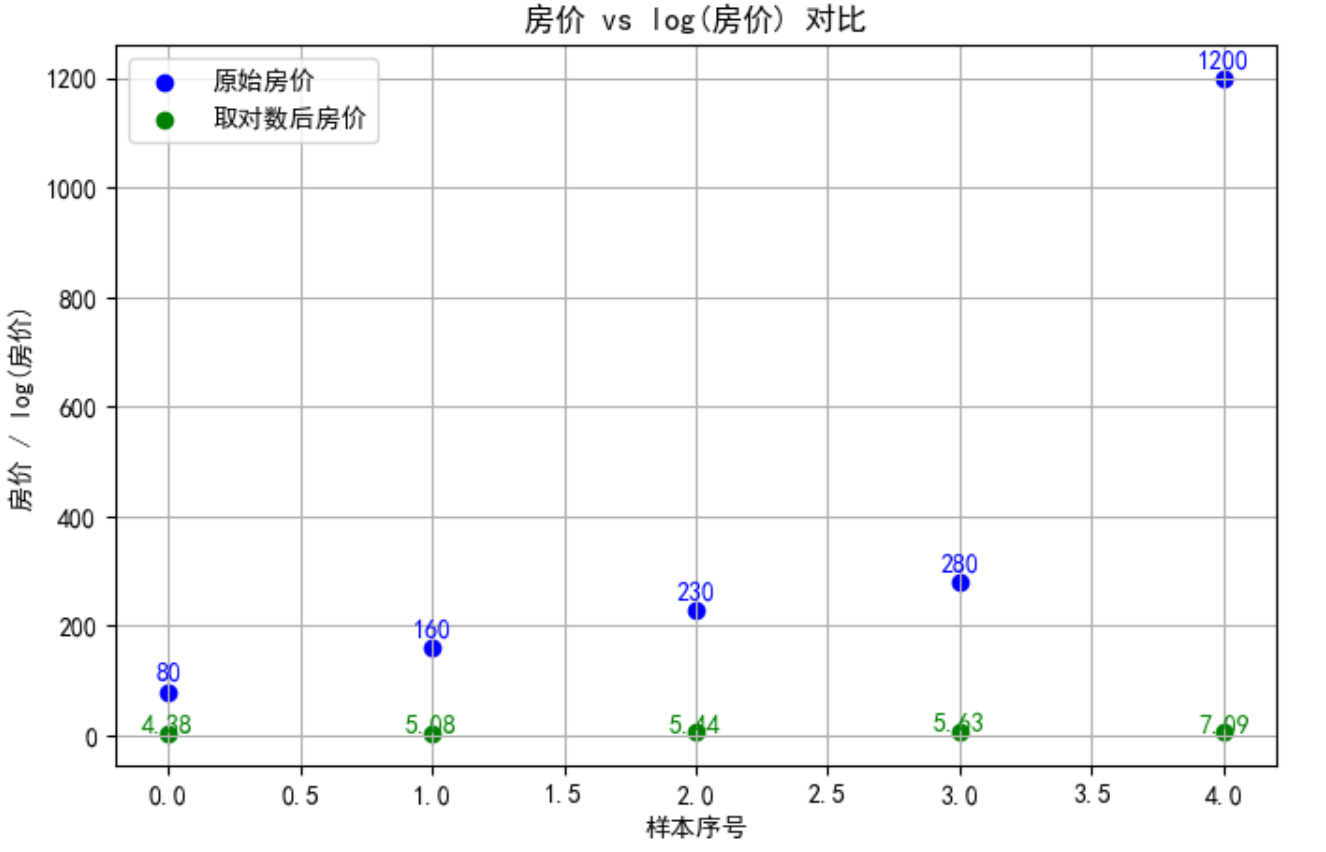

多元线性回归
假设目标变量 $y$与自变量 $x$存在线性关系:
$y=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_px_p+\epsilon$
$y$ : 因变量(目标变量)
$x_1,x_2,…,x_p$: 自变量(特征)
$\beta_0$: 截距
$\beta_1,\beta_2,…,\beta_p$: 回归系数,表示自变量对$y$ 的影响大小
$\epsilon$ : 误差项
如果用矩阵表示
$Y=X\beta +\epsilon$
依然用最小二乘法来估计,目标还是最小化误差平方和$Q(\beta_0,\beta_1,\beta_2,…,\beta_p)=\sum_{i=1}^{n}(y_i-{\beta_0}-\beta_1x_1-\beta_2x_2-…-\beta_px_p)^2$ 。那么还会出现同样的问题,如果有一个极端值出现,平方和依然会放大误差。此时,各个回归系数都有可能发生改变。
举例
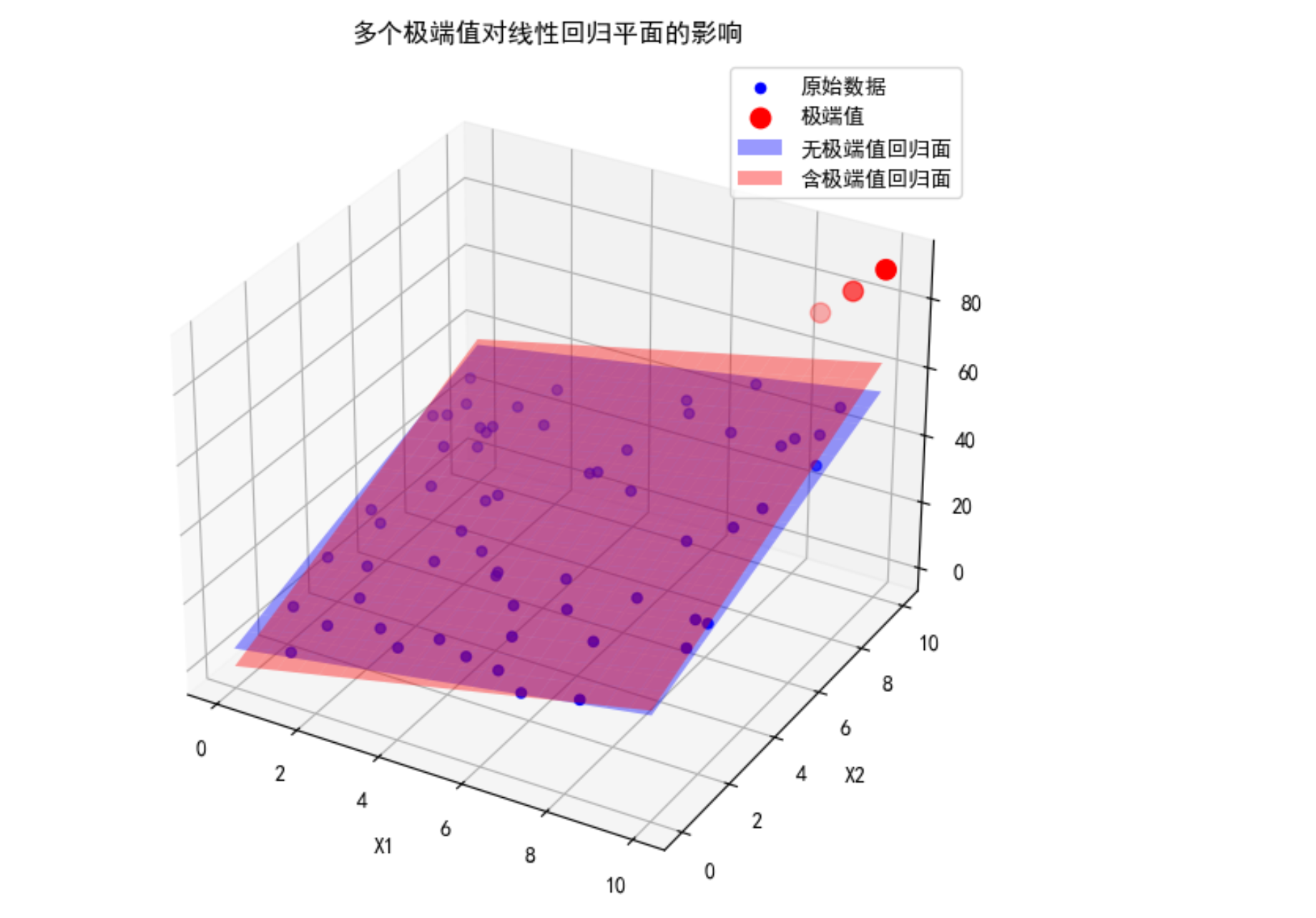
假设回归平面是二维的,目标变量 $y$与自变量 $x$存在线性关系:
$y=\beta_0+\beta_1x_1+\beta_2x_2+\epsilon$
则数据是沿着某个平面分布的,一个极端值就是一个远离平面的点,为了使误差平方和达到最小,远离平面的点会“拉动”拟合平面向自己靠近。
在房价预测模型中,现在假设房价和居住面积大小、房龄两个因素有关。
| 样本 | 面积 (㎡) | 房龄 (年) | 房价 (万元) | 备注 |
|---|---|---|---|---|
| 1 | 50 | 1 | 120 | 正常 |
| 2 | 60 | 3 | 130 | 正常 |
| 3 | 70 | 5 | 145 | 正常 |
| 4 | 80 | 2 | 160 | 正常 |
| 5 | 90 | 4 | 175 | 正常 |
| 6 | 100 | 6 | 190 | 正常 |
| 7 | 110 | 3 | 210 | 正常 |
| 8 | 120 | 5 | 230 | 正常 |
| 9 | 130 | 1 | 250 | 正常 |
| 10 | 100 | 10 | 1200 | 极端高价 |
最后一套属于极端值。
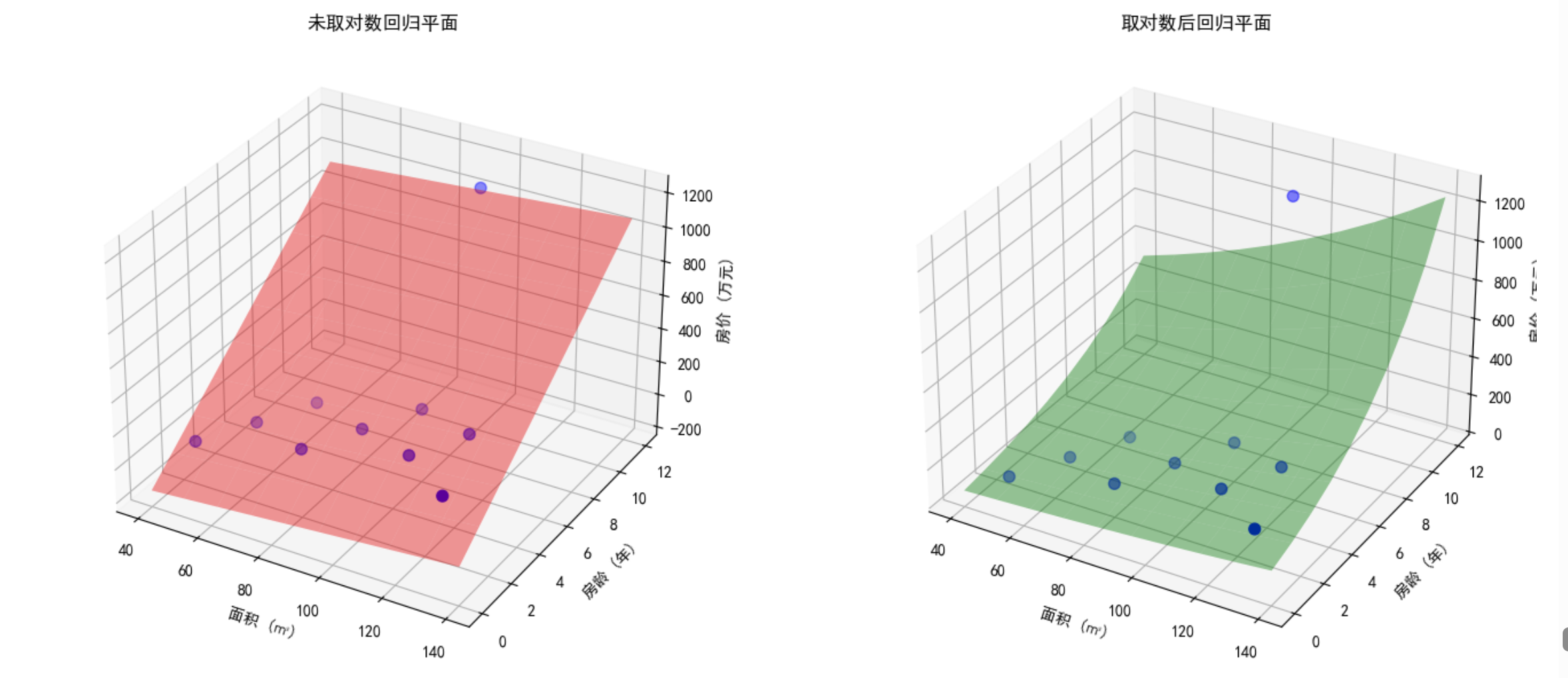
未对极端值处理之前,极端值把平面拉的很高,导致大部分普通房被高估。处理之后,极端值被压缩,回归平面更贴近大多数正常值。
总结
-
最小二乘对异常值十分敏感。
-
线性回归方法依赖最小二乘估计回归系数,因此极端值会显著影响线性回归结果,在预测前要对极端值进行处理。
参考资料
[1] 茆诗松等. 概率论与数理统计教程
[2] Anne Kowalskie. The Impact of Outliers on Linear Regression Models: Detection and Correction Strategies. June 2025OTS Canadian Journal 4(6):108-118. 链接:The Impact of Outliers on Linear Regression Models
图例代码地址:代码
